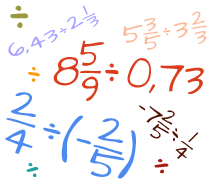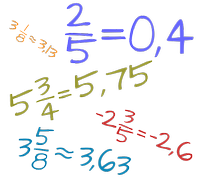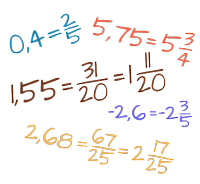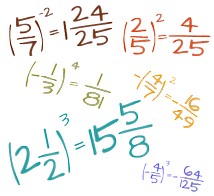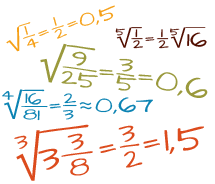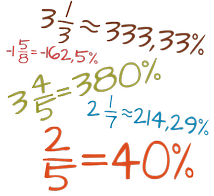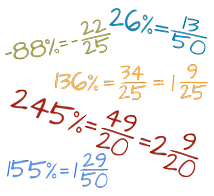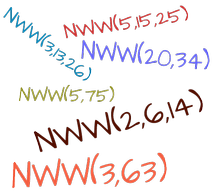Wszystko o ułamkach, działania na ułamkach, zadania, wyjaśnienia, kalkulatory ułamków

Znajdziesz tu całą wiedzę o ułamkach zwykłych i dziesiętnych, przykłady zadań i szczegółowe wyjaśnienia wykonywanych czynności krok po kroku w wielu kalkulatorach z ułamkami. Dodatkowo masz do dyspozycji kalkulator ułamków, za którego pomocą dokonasz dowolnych obliczeń na ułamkach zwykłych i dziesiętnych. Dodawanie, odejmowanie, mnożenie, dzielenie, potęgowanie i pierwiastkowanie ułamków, zamiana ułamków na dziesiętne, zwykłe, mieszane, na procenty i wiele innych.

Kalkulatory ułamków


Szybki kalkulator ułamków

Ułamek dziesiętny wpisz w pole liczby całkowitej. Jeśli jest to ułamek właściwy lub niewłaściwy a jego wartość jest ujemna znak minus wstaw przy liczniku.



Oblicz

Kalkulator dodawania ułamków

Kalkulator dodawania krok po kroku z wyjaśnieniami

Kalkulator odejmowania ułamków

Kalkulator odejmowania ułamków krok po kroku z wyjaśnieniami

Kalkulator mnożenia ułamków

Kalkulator mnożenia ułamków krok po kroku z wyjaśnieniami


Kalkulator dzielenia ułamków

Kalkulator dzielenia ułamków krok po kroku z wyjaśnieniami

Zamiana ułamka zwykłego na dziesiętny

Zamień ułamek zwykły na ułamek dziesiętny

Zamiana ułamka dziesiętnego na zwykły

Zamień ułamek dziesiętny na ułamek zwykły


Kalkulator potęgowania ułamków

Kalkulator ułamków - podnoszenie ułamków do potęgi z wykładnikiem całkowitym

Kalkulator pierwiastkowania ułamków

Kalkulator ułamków - pierwiastkowanie ułamków zwykłych i liczb mieszanych

Kalkulator zamiany ułamków zwykłych na procenty

Zamień ułamek zwykły na wielkość wyrażoną w procentach


Kalkulator zamiany procentów na ułamek zwykły

Zamień wielkość wyrażoną w procentach na ułamek zwykły

Kalkulator najmniejszej wspólnej wielokrotności

Oblicz najmniejszą wspólną wielokrotność dla dwóch lub więcej liczb

Kalkulator największego wspólnego dzielnika

Znajdź największy wspólny dzielnik dla dwóch lub więcej liczb

Wszystko o ułamkach

$$\mathsf{\frac{a}{b}}$$

Co to są ułamki niewłaściwe, właściwe, liczby mieszane i ułamki dziesiętne?

Ułamki dziesiętne, niewłaściwe, właściwe i liczby mieszane.
Zobacz co to są i czym się różnią ułamki dziesiętne, niewłaściwe, właściwe i liczby mieszane.

¾?
$$\mathsf{+}$$

Jak dodawać ułamki?

Dodawanie ułamków zwykłych i dziesiętnych.

Zobacz jak dodawać liczby mieszane, ułamki dziesiętne i ułamki zwykłe o wspólnych i różnych mianownikach za pomocą kilku metod - sposobem szybkim, prostym i tradycyjnym.

+
$$\mathsf{-}$$

Jak odejmować ułamki?

Odejmowanie ułamków zwykłych i dziesiętnych.

Zobacz jak odejmować liczby mieszane, ułamki dziesiętne i ułamki zwykłe o wspólnych i różnych mianownikach za pomocą kilku metod - sposobem szybkim, prostym i tradycyjnym.

−
$$ \mathsf{\times} $$

Jak mnożyć ułamki?

Mnożenie ułamków zwykłych i dziesiętnych.

Zobacz jak mnożyć ułamki zwykłe o takich samych i różnych mianownikach oraz ułamki dziesiętne.

×
$$\mathsf{\div}$$

Jak dzielić ułamki?

Dzielenie ułamków zwykłych i dziesiętnych.

Zobacz jak dzielić ułamki zwykłe o takich samych i różnych mianownikach oraz ułamki dziesiętne.

÷
$$ \mathsf{\bigl(\frac{a}{b}\bigr)^n}$$

Jak potęgować ułamki?

Potęgowanie ułamków zwykłych i dziesiętnych.

Zobacz jak podnieść do dowolnej potęgi ułamki zwykłe, liczby mieszane oraz ułamki dziesiętne.

(¾)²
$$ \mathsf{\sqrt[n]{\frac{a}{b}}} $$

Jak pierwiastkować ułamki?

Pierwiastkowanie ułamków zwykłych i dziesiętnych.

Zobacz jak wyciągnąć pierwiastek dowolnego stopnia z ułamka zwykłego, liczby mieszanej oraz ułamka dziesiętnego.

√¾
$$\mathsf{⇄}$$

Jak zamienić liczby mieszane na ułamki?

Zamiana liczb mieszanych na ułamki zwykłe.

Zobacz jak łatwo zamienić liczby mieszane na ułamki zwykłe niewłaściwe.

⇄
$$\mathsf{⇄}$$

Jak zamienić ułamki niewłaściwe na liczby mieszane?

Zamiana ułamków niewłaściwych na liczby mieszane.

Zobacz jak w prosty sposób zamienić ułamki niewłaściwe na liczby mieszane.

⇄
$$\mathsf{⇄}$$

Jak zamienić ułamki dziesiętne na ułamki zwykłe ?

Zamiana ułamków dziesiętnych na ułamki zwykłe i liczby mieszane.

Zobacz jak w prosty sposób zamienić ułamki dziesiętne na ułamki właściwe, niewłaściwe i na liczby mieszane.

⇄
$$\mathsf{⇄}$$

Jak zamienić ułamki zwykłe na ułamki dziesiętne?

Zamiana ułamków zwykłych oraz liczb mieszanych na ułamki dziesiętne.

Zobacz jak w prosty sposób zamienić ułamki zwykłe właściwe i niewłaściwe oraz liczby mieszane na ułamki dziesiętne.

⇄

Ostatnio wykonywane obliczenia

$$\style{}{NWD(24,42) = 6}$$$$\frac{35}{100}\style{}{=35 \text{%}}$$$$\style{}{NWD(5,21) = 1}$$$$6\frac{3}{5}+7\frac{5}{8}$$$$0\frac{24}{20}\style{}{=1.2}$$$$8.5\text{%}= \style{}{}\style{}{\frac{17}{200}}$$$$-14.008=\style{}{- \frac{1751}{125}} = \style{}{-14 \frac{1}{125}}$$$$\style{}{NWD(23,60) = 1}$$$$\style{}{NWD(25,52) = 1}$$$$64.51\text{%}= \style{}{\frac{6451}{10000}}$$$$4.176=\style{}{ \frac{522}{125}} = \style{}{4 \frac{22}{125}}$$$$\sqrt[3]{64\frac{3}{3}}=\style{}{\sqrt[3]{65}}\approx \style{}{4.0207}$$$$\style{}{NWD(10,18) = 2}$$$$\frac{8}{18}+\frac{1}{14}$$$$90·\frac{7}{15}$$$$\frac{88}{84}÷\frac{11}{12}$$$$6349281$$$$64\frac{1}{4}+46\frac{1}{3}$$$$\frac{897}{1594}\style{}{≈56.27 \text{%}}$$$$\style{}{NWD(10,18) = 2}$$$$2.5÷\frac{1}{2}$$$$\frac{15}{8}\style{}{=187.5 \text{%}}$$$$0\frac{1}{6}\style{}{≈16.67 \text{%}}$$$$\style{}{NWW(5,27) = 135}$$$$156.25\text{%}=\style{}{ \frac{25}{16}} = \style{}{1 \frac{9}{16}}$$$$\sqrt[1]{\frac{121}{441}}= \style{}{\frac{121}{441}} \approx \style{}{0.2744}$$$$\frac{1}{2}·\frac{13}{45}$$$$\frac{3}{3}+\frac{6}{7}$$$$\style{}{NWW(1,175) = 175}$$$$(2\frac{3}{1})^{0}= \style{}{1}$$$$3\frac{1}{2}+8\frac{1}{2}$$$$3\frac{13}{60}+\frac{1}{4}$$$$\sqrt[4]{\frac{18}{15}}=\style{}{\frac{\sqrt[4]{750}}{5}}\approx \style{}{1.0466}$$$$8\frac{18}{25}\style{}{=8.72}$$$$68.69\text{%}= \style{}{\frac{6869}{10000}}$$$$(0\frac{9}{10})^{1} = \style{}{0}\frac{\style{}{9}}{\style{}{10}}$$$$\frac{69}{114}÷14$$$$3\frac{1}{3}+1\frac{2}{3}$$$$\sqrt[3]{\frac{1}{81}}=\style{}{\frac{1\sqrt[3]{9}}{9}}\approx \style{}{0.2311}$$$$(\frac{7}{2})^{6}= \style{}{}\style{}{1838} \frac{\style{}{17}}{\style{}{64}}$$$$\frac{1}{10}+\frac{1}{20}$$